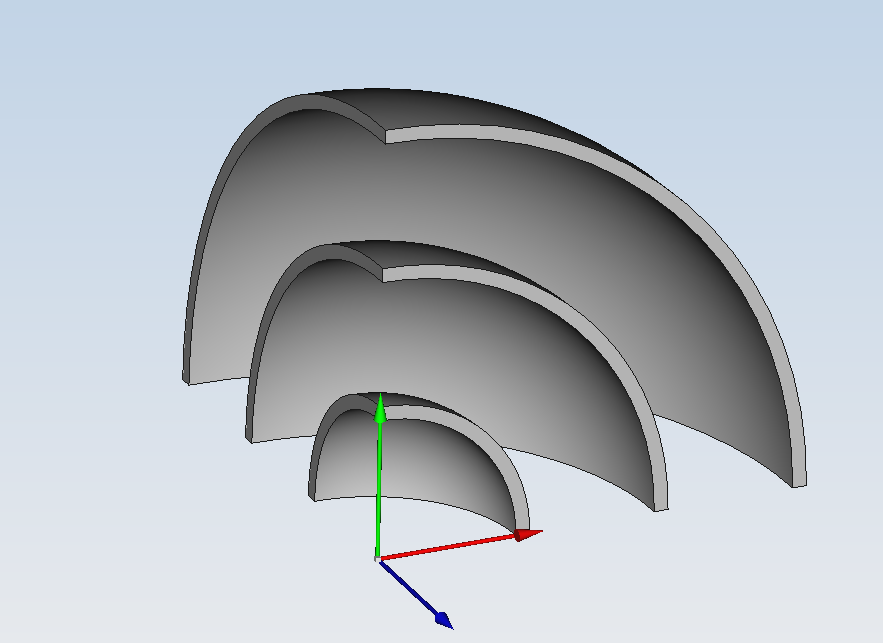
几何

三层球壳，球壳内半径分别为1 m、2 m、3 m；球壳厚度均为0.1 m。分别采用case1 三维实体模型和case2轴对称模型建模。由于对称性，三维实体仅建立1/8模型。

网格

轴对称模型采用二阶四边形轴对称单元，三维实体采用一阶六面体（包含部分三棱柱）单元。

材料

材料导热系数均为 1 W/(m*K)。

边界条件

稳态分析，初始温度设置为 300 K，绝对零度设置为 0 K，Stefan-Boltzmann常数设置为 5.67e-8 W*m^-2*K^-4；

内球壳内表面设置 100 W/m^2的表面热流密度；外球壳外表面设置表面对流，对流换热系数5 W/(m^2*K)，冷源温度 300 K，其它表面设置腔体辐射，发射率为 0.45，闭合腔体。

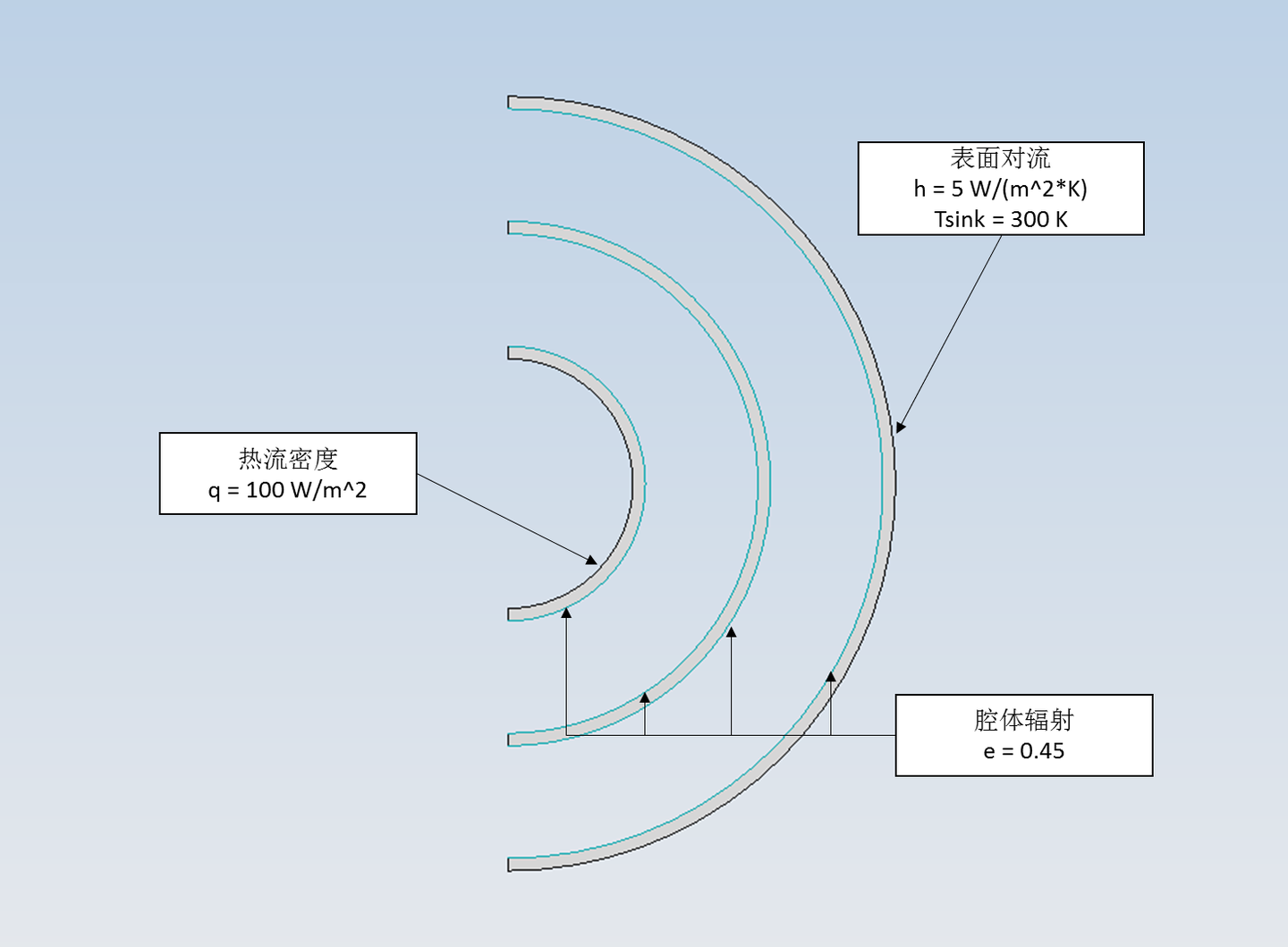
三维由于只建了1/8模型，需要设置辐射对称，即将腔体辐射打开关于yz平面、zx平面和xy平面的对称。

二、计算结果

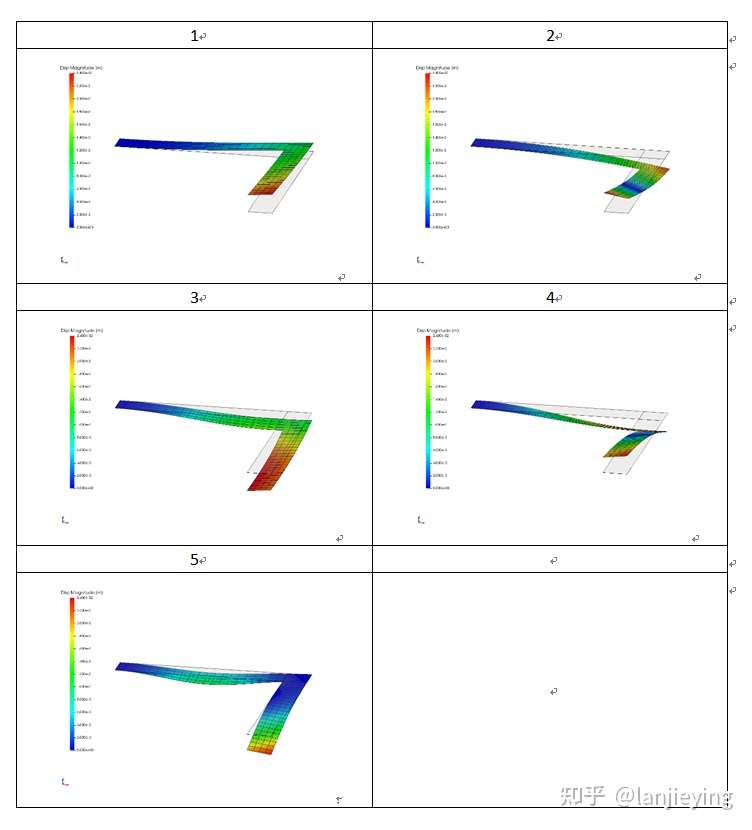
轴对称模型温度云图：

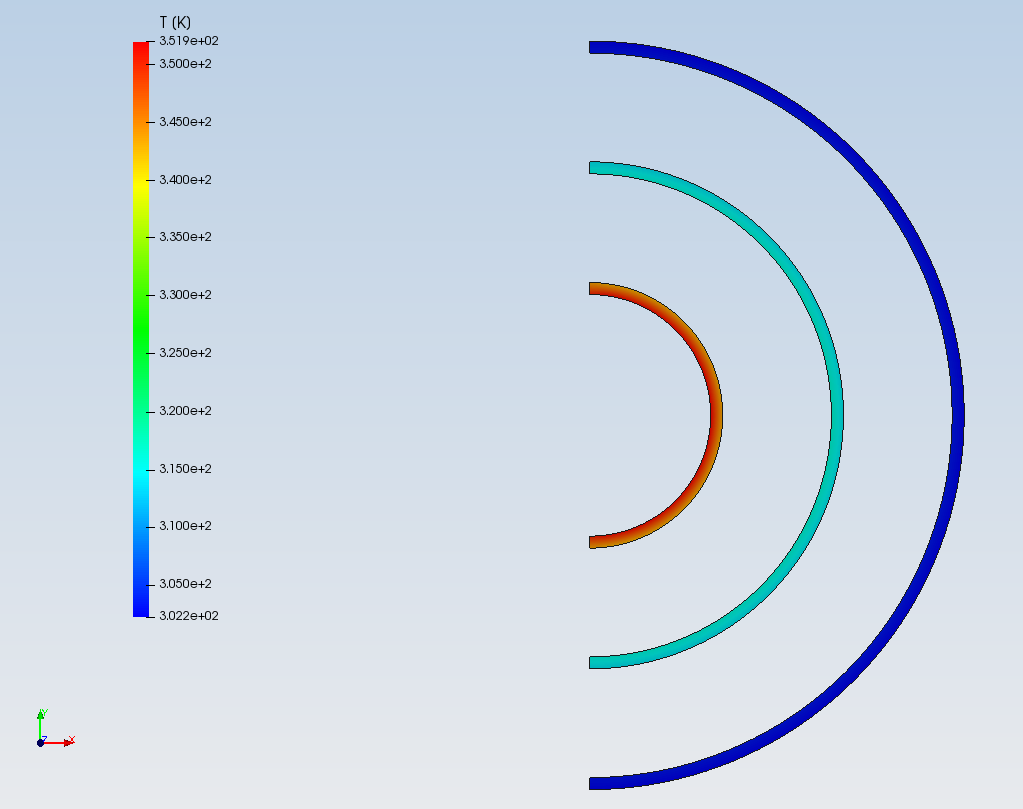
三维模型温度云图：

仿真得到内壁最大温度约351K，外壁温度约302K，两种方法的计算结果基本一致，最大值误差约0.25%，有兴趣的网友可以用其他商业软件验证本例。

由求解器log可知，辐射角系数矩阵按行求和的最大和最小值均为1.0。

三、腔体辐射功能简介

新版的Simdroid热分析增加了腔体辐射的计算功能，腔体辐射也叫做面面辐射，一般用于计算物体不同表面之间的辐射换热，面面间辐射采用灰体辐射假设，考虑的计算假设包括：

（1）所有表面不透明，即透射率为0；

（2）同一个单元表面上温度均匀；

（3）同一个单元表面上材料性质均匀；

（4）发射率等于吸收率，并等于1减去反射率，即

（5）所有能量的发射和反射均为散射（diffusely）；

（6）表面热通量在单元表面上均匀分布。

腔体辐射的控制方程为：

其中下标和为表面序号，为辐射角系数，为温度，为表面面积，为发射率，为斯特藩-玻尔兹曼常数，为一个表面上的总热通量。

Simdroid软件支持三种辐射求解方法：（1）消去法，（2）半隐式迭代法，（3）显式迭代法。其中消去法为热传导方程和辐射方程完全耦合求解，它将辐射自由度在系统方程中隐式消去，采用完全牛顿法求解，因为考虑了准确的非对称切线刚度，其求解精度最高且所需迭代次数最少，但单步求解耗时极长。显式迭代法则将两个方程分开迭代求解，其单步求解最快，但对于一些除外辐射边界后的不定问题（即缺少足够的边界约束，本例即为这种情况）可能不收敛。半隐式迭代法介于两者之间，并可以提供足够的约束。

由于辐射方程求解时需要求解一个稠密矩阵，表面自由度过多会严重降低稠密方程的求解效率，此时建议将不存在可视条件的表面分到不同腔体中。例如本例的四个辐射表面，只有两两之间存在可视，即可以拆成两个腔体分开求解。

Simdroid软件支持三种辐射角系数的计算方法：（1）半球/半立方投影法，（2）射线追踪法，（3）周线积分法。当问题为二维时，出平面方向被考虑为无限长，此时方法（1）自动退化为半球投影，其它情况均为半立方投影。方法（1）和（2）可以求解存在辐射遮挡的情况，由于采用了近似计算方法，对于两个大表面间的辐射角系数的计算存在一定误差；方法（3）为半解析方法，其可以精确计算出任何表面间的辐射角系数，但其不能考虑辐射遮挡，固本例不适用。方法（2）和（3）只支持三维模型，当模型为二维或二维轴对称时，必须选择方法（1）。

当腔体为闭合腔体时，即每个表面的所有方向均可以“看见”其它表面，辐射角系数矩阵按行求和应为1.0；当为非闭合腔体时，会发生部分对环境的辐射，此时Simdroid需要用户输入辐射的环境温度。

当问题中存在任何对称，例如本例的轴对称和平面对称，Simdroid求解器在计算辐射角系数时会自动考虑对称性，此时每个表面存在看见自己的情况。

Simdroid软件中的材料常数、发射率、对流换热系数、热流密度等可以设置温变曲线；冷源温度、辐射环境温度等可以设置时变曲线。指定温度等边界条件同时也可以设置坐标相关的分布函数。